GEOMETRY

Geometry: Triangle Inequality

We will discuss two commonly used inequality relationships in a triangle: the Triangle Inequality Theorem and the Angle-Side Relationship.




Triangle Inequality Theorem

The Triangle Inequality theorem states that the sum of the lengths of any two sides of a triangle is greater than the length of the third side.

triangle

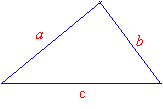
For the above triangle:

a + b > c
b + c > a
a + c > b





Example 1: Find the range of values for s for the given triangle.

triangle

Solution:

Step1: Using the triangle inequality theorem for the above triangle gives us three statements:

s + 4 > 7 ⇒ s > 3
s + 7 > 4 ⇒ s > –3 (not valid because lengths of sides must be positive)
7 + 4 > s ⇒ s < 11

Step 2: Combining the two valid statements:

3 < s < 11

Answer: The length of s is greater than 3 and less than 11





The following video describes triangle inequality.

The following video shows the conditions required to draw a triangle.




Angle-Side Relationship

In a triangle, the side opposite the larger angle is the longer side.

Example 1: Compare the lengths of the sides of the following triangle.

triangle

Solution:

Step1: We need to find the size of the third angle. The sum of all the angles in any triangle is 180º.

∠A + ∠B + ∠C = 180°
⇒ ∠A + 30° + 65° = 180°
⇒ ∠A = 180° - 95°
⇒ ∠A = 85°

Step 2: Looking at the relative sizes of the angles.

∠B < ∠C < ∠A

Step 3: Following the angle-side relationship we can order the sides accordingly. Remember it is the side opposite the angle.

AC
Answer: AC